מגזין ברידג' בניהול ובעריכת גבי לוי
פורסם ביום: 23.02.2023; עודכן ביום: 03.09.2024
קהל היעד:
וכעת, כתבה חדשה " העיקרון של המקומות הפנויים-The theory of vacant places "
המידע באתר מנוסח בלשון זכר לצורכי נוחות בלבד, ומתייחס לגברים ולנשים כאחד.
העיקרון – התיאוריה ידועים גם בשם Vacant Spaces.
לכניסה לאווירה, הציטוט " Lady Gaga : " I like black because it is a vacant space.
לקישור ל " George Maple – Vacant Space [A Live Recording] " – לחץ כאן
ומצד שני, לקישור ל " Fargo: The Law Of Vacant Places " – לחץ כאן
עפ"י ה-dbpedia: בתחילת חלוקת הקלפים, כל אחת מ-4 הידיים כוללת 13-קלפים ואפשר לומר שיש 13 מקומות פנויים בכל יד. ההסתברות שקלף מסוים נמצא ביד מסוימת היא רבע, או 13/52, שיעור המקומות הפנויים ביד זו. מנקודת המבט של שחקן שרואה יד אחת, הסיכוי הסביר של קלף חסר באחת מהידיים האחרות הוא שליש. עיקרון המקומות הפנויים הוא כלל לעדכון ההסתברויות האחידות הללו כאשר לומדים על החלוקה במהלך המכרז והמשחק. בעיקרו של דבר, ככל שהמיקומים של חלק מהקלפים נודעו – במיוחד כשההתפלגות השלמה של חלק מהסדרות נודעות – הסיכויים למיקומו של כל קלף מסוים אחר נשארים פרופורציונליים למספרים ההולכים ומתמעטים של קלפים לא מזוהים בכל הידיים, כלומר למספרים של קלפים מסוימים-נקרא מקומות פנויים. עקרון המקומות הפנויים נובע מתורת ההסתברות המותנית, המבוססת על משפט Bayes.
עפ"י Don Sondergeld: התיאוריה של מקומות פנויים בברידג' קובעת שכאשר התפלגות-חלוקה של סדרה אחת או יותר ידועה לחלוטין, ההסתברות שיריב מחזיק קלף מסוים בכל סדרה אחרת עומדת ביחס ישר למספר המקומות הפנויים שנותרו בידיהם בהתאמה.
לקישור – לחץ כאן
עפ"י greatbridgelinks: ה-Theory of Vacant Spaces, למשל, הוא מונה הסתברות בשימוש נרחב בברידג' – זהו מדד פשוט לאמוד את מיקומו של קלף בידיים שחולקו. ניתן ליישם את התיאוריה על כל שילוב של קלפים כדי להעריך את הפיצול הסביר.
ועפ"י מספר מקורות: במשחק הברידג', החוק או העיקרון של מקומות פנויים הם שיטה פשוטה להערכת המיקום הסביר של כל קלף מסוים ב-4 הידיים. זה יכול לשמש הן כדי לסייע בהחלטה ליד השולחן והן כדי לגזור את כל טבלת ההסתברות לחלוקת הסדרות. עקרון המקומות הפנויים (VS) הוא כלי שימושי נוסף ל-Restricted Choice (RC), בידיו של כרוז מיומן. ההבדל העיקרי הוא שה-VS תלוי במידע לא מהסדרה עצמה אלא במידע על סדרות אחרות. הביצוע שלו פשוט בתנאי שצריך לאתר רק קלף בודד וניתן להציג את המידע על סדרות אחרות בצורה פשוטה.
ולעצם העניין, עפ"י Jill Courtney המנוחה שייצגה את אוסטרליה בנבחרות הנשים במזרח הרחוק ב-1987 וב-1992, ב-Venice Cup ב-1987 ובקבוצות האולימפיאדה לנשים ב-1992.
החלוקה הראשונה:
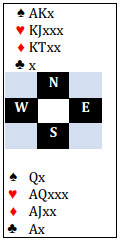
הכותבת מדגישה שזה כמו כל ספירה, תהליך אבולוציוני. ככל שתקבל מידע נוסף דברים עשויים להשתנות. בואו נסתכל קודם על מצב A priori-מִלְכַתְחִילָה. הכרזתם לחוזה המצוין של ♥7 ללא הפרעה.
קלף club מובל ואתה משחק על שליטים ומגלה שאתה צריך לשחק שלושה סיבובים כמו שמזרח מופיע בסיבוב הראשון. הוא משליך שלושה קלפי clubs. חמוש בידע שלך על חלוקת סדרת ה-hearts אתה יכול כעת ליישם את העיקרון של מקומות פנויים. בידו של מזרח אתה יודע יש 13 מקומות פנויים בעוד שבידו של מערב יש רק 10. (הובלות ה-clubs וההשלכות שלהם אינם רלוונטיים בשלב זה). רק סדרת ה-heart חשובה כרגע. זה אומר, בהתבסס על עקרון המידתיות הישירה שלנו, שהקלף החסר המכריע –♦Q הוא בעדיפות של 13-10 להיות בידו של מזרח.
אבל בואו נעשה את הדברים קצת יותר מסובכים. ביד זאת אין למהר לבדוק את סדרת ה-diamonds אז אנחנו יוצאים למסע גילוי. אנחנו חותכים club וכולנו עוקבים (אז שום דבר לא שינה את הסיכויים שלנו) ואז אנחנו גובים שלושה סיבובים של spades. תארו לעצמכם שבסיבוב השלישי של spades, מערב כעת משליך club. כעת יש לך חלוקה מלאה של סדרה שנייה. ידוע שמערב התחיל עם שלושה hearts ועכשיו שני spades ושני clubs, מה שמשאיר אותו עם שישה מקומות פנויים. ידוע שיש למזרח חמישה clubs ושישה spades ושמותירים לו שני מקומות פנויים. פתאום הסיכויים עברו באופן קיצוני מ-13-10 מול מערב שמחזיק את ה-Q הזו ל-6-2 לטובת-בעד. זה, מעל לכל, מדגיש את החשיבות של משחקי גילוי כאשר יש לך את המותרות לבדוק את כל החלוקות. אבל שים לב שאם אינך מקבל סימן-אינדיקציה ברורה שכזו כפי שה-spades מראה, אתה עדיין צריך ללכת עם הסיכויים 13-10 לטובת עקיפת מזרח.
זוהי דוגמה שנייה לטכניקת המקומות הפנויים שלנו, לפיה לא רק שנוכל לנחש ניחוש מושכל אלא גם לחשב את הסיכויים המדויקים (בהיעדר שיקולי הכרזות) בהתבסס על הנחות אלו.
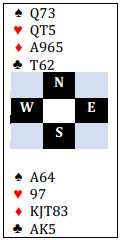
אתה בהכרזה חופשית 3NT ומערב מוביל את ה-J spade עליו אתה משחק קלף נמוך וה-K מופיע. ברור שאתה זוכה עם ה-A ועכשיו משחק קלף diamond נמוך ל-A שעליו עוקבים 2 המגנים. אתה ממשחק עוד diamond ומזרח עוקב בקלף נמוך. כאן אנחנו צריכים לבחון המצב היטב ולגבש דעה לגביו, כדי שנוכל להחליט מה לעשות. המשחק ללקיחה הראשונה הצביע על כך שלמערב יש שישה spadrs ועכשיו לפחות diamond אחד. מזרח, לעומת זאת, הראה spade אחד ושני diamonds עד לנקודה זו. לכן יש למערב שישה מקומות פנויים ואילו למזרח יש עשרה (spade אחד ושני diamonds שוחקו). בואו נקבל שוב את המדריך היחסי הישיר שלנו – הסיכוי שה-Q diamonds תהיה עם מזרח הם בדיוק 10-6. באחוזים (תודה מר Kelsey) זה 62.5%.
לקישור לשיעורה " Vacant Places " – לחץ כאן
עפ"י Neil H. Timm: אין באמת קסם בשימוש בתיאוריית המקומות הפנויים; ההסתברויות אינן יותר מיחס השילובים-הצירופים.
יש לך בסך הכול 9 קלפים בסדרת השליט ואתה רוצה למצוא את ה-Q. האם אתה עוקף או משחק למען הפלה? A priori ללא מידע מההכרזות, רבים משתמשים בכלל של 8 תמיד 9 לעולם לא-. זאת עקיפה עם 8 ומשחק על הפלה עם 9. האחוזים של כל אחד מהם הוא 50% לעומת 52.18%. עם זאת, מתי כלל זה לא עובד? פשוט, כאשר יש לך מידע נוסף מההכרזות.
לקישור לשיעורו " Finding the Q using Vacant Places " – לחץ כאן
וגם: הקשיבו להכרזות: לדוגמה, נניח שיריב ביצע הכרזת מנע-pre-empt המראה סדרת 7-קלפים, אז נותרו בידו 6 'מקומות פנויים' לקלפים בסדרות אחרות בעוד שאם לכרוז ולדומם יש יחד 4 קלפי clubs למגן השני יש 2 קלפי clubs שמותיר 11 מקומות פנויים ביד הזאת. אם יש 4 קלפים בסדרה אחרת (נניח hearts) בידיים האלה, ההסתברות שהם יחלקו 2-2 נעות בין מעל ל-40% לפחות מ-35% בעוד שהיד עם יותר מקומות פנויים בסבירות גבוהה פי 5 מהאחרת להחזיק 3 או 4 קלפי hearts.
לקישור לשיעורו בכותרת " Some Useful Bridge Probabilities " – לחץ כאן
לקישור לשיעור " Relevant Percentages for Bridge Players " – לחץ כאן
עפ"י ניתוח יד של Bob Mackinnon בכותרת " The Matchpoint Anti-Finesse ": כלל הזהב חל באופן שווה בעת קבלת החלטת משחק. לעתים קרובות זה מצטמצם לדייג ל-Q. שחקנים רבים מרגישים שהם חייבים לקחת את כל הלקיחות הזמינות בחוזה נפוץ, כך יהיה עקיפות בכל הזדמנות. המשחק עשוי להתדרדר לטירוף של עקיפה שהכרוזים אינם מוכנים לוותר על הלקיחה הנוספת שתושג כאשר העקיפה במקרה מצליחה. הם משחקים כדי למקסם את מספר הלקיחות שנלקחו, ואם העקיפה תיכשל זה לא יעלה כל כך הרבה עם רוב המשחקים באותו אופן. עם זאת, לא צריך לקחת עקיפה שיש סיכוי גבוה יותר שתיכשל מאשר לא. היד הבאה ששיחקה לאחרונה במועדון המקומי מייצגת מצב שבו כרוז עושה הכי טוב בכך שהוא מחליט נגד עקיפה.
מערב הכריז 1NT overcall מעל הכרזת הפתיחה של ♥1, לא בחירה של כולם. השותף עורר את ה-stayman ואז עזב אותו ב-2NT. הובלת הפתיחה היתה ♥T והועלו שאלות בשולחן מדוע מזרח לא העלה ל-3NT. עם זאת, נראה שהזהירות שלו הייתה מוצדקת מכיוון ש-8 לקיחות עשויות להיות הגבול בגלל חלוקת הקלפים. דרום לקח את ♥A שלו והמשיך ב-heart נמוך אל ♥K וה-LHO-היריב מצד שמאל עקב עם ♥9. בשלב זה לדרום היו 3 לקיחות heart לעשות אם וכאשר ייכנס שוב להובלה. אחד היתרונות העיקריים של הכרוז הוא שבראותו את הדומם הוא יודע מיד את חלוקת הצדדים. כאשר חלוקת הצדדים היא 7-7-6-6, לעתים קרובות משתלם לכרוז לנקוט במשחק פסיבי ולוותר מוקדם על המפסידים הברורים במקום לנסות ליצור מנצח נוסף בכוח. לפעמים מופעל לחץ בצורה זו. הגישה הפעילה-האקטיבית היא לעקוף את ה-♠Q בדומם כדי לקחת את עקיפת ה-club. אם היא מצליחה, המשך ב-clubs ייצר 9 לקיחות בתנאי שה-RHO יחזיק ♣ Qx(x). אם העקיפה מפסידה, עדיין יש סיכוי מצוין לקחת 8 לקיחות, באמצעות 2 spades, קלף heart אחד, diamond אחד ו-4 clubs.
השאלה שיש לשאול היא האם עקיפת ה-club צפויה להצליח או לא. ע"י לקיחה-מעל-overtaking עם ♠A, מספר לקיחות ה-spade מצטמצם מ-3 ל-2, כך שהכרוז צריך לבצע לקיחה נוספת ב-clubs כדי לפצות על ההפסד. מה הסיכויים שהעקיפה תצליח? להכרזת פתיחת המושב הראשון שלו דרום צריך את ♦K ולפחות Q אחת בסדרת minor. עם 15 HCP הוא עשוי היה לפתוח 1NT. לצפון יש 11 מקומות פנויים ל-7 של דרום, כך שהסיכוי שדרום יחזיק ב-Q♣ הוא פחות מ-50%. זה מציין שהכרוז צריך להימנע מהעקיפה. בואו נסתכל על חלוקת הסדרות הסבירה ביותר. שני המועמדים העיקריים הם צפון 4=2=4=3 מול 3=5=2=3 וצפון 4=2=3=4 מול 3=5=3=2. אם ה-clubs מחולקים 3-3, זה 50-50 בין אם העקיפה מצליחה או לא. אם ה-clubs יתחלקו 4-2, כנראה שהעקיפה תיכשל. מכיוון שהצורות סבירות באותה מידה, לא סביר שהכרוז ישיג את הניקוד שלו על ידי נטילת עקיפת ה-club. מהי התוכנית החלופית? הכרוז יכול לפדות את ה-♠KQ ולשחק את ה-♣J בתקווה שצפון חייב לקחת את ה-♣Q. אם כן, לכרוז יש 9 לקיחות בקלות. צפון חייב להתחמק על ה- ♣J אם הוא מחזיק ארבע ל-Q כדי להרוס את התקשורת עם הדומם ולהחזיק את הכרוז על 8 לקיחות. אבל חלקם עשויים לנצח בהזדמנות הראשונה ולצאת 'בבטחה'. זה יתרון שניתן לנצל. מצד שני, אם לדרום יש את ה-♣Q, הכרוז מוחזק ל-8 לקיחות באופן מידי. זו תהיה סיבה לשמחה כללית בשולחן אם דרום יחזיק ב-Q♣ singleton, בכל זאת 8 לקיחות עדיין יילקחו כשהתקשורת של הכרוז עדיין שלמה.
מה היה המצב ליד השולחן? באופן לא מפתיע הצורה של צפון הייתה אחד מ-2 המועמדים הסבירים ביותר, 4=2=3=4, והוא החזיק ב-Q♣ כצפוי במצב זה. זה בדיוק מה שהכרוז עשוי היה לצפות בלקיחה השנייה בעקבות קו ההיגיון המוצע. בכך שלא לקח עקיפה מפסידה, יכול להיות שמערב עדיין יקלע 9 לקיחות בסיכוי הנוסף של הגנה גרועה. קשה לנחש כמה matchpoints תהיה שווה לקיחת היתר-overtrick.
לקישור – לחץ כאן
לקישור לשיעור באתר " automaton " – לחץ כאן
עפ"י Karen Walker: אם אינך יודע כיצד הסדרה מתחלקת, השתמש בתיאוריה של "מקומות פנויים" כדי לקבוע לאיזה יריב סביר להניח שיהיה אורך גדול יותר בה. נניח שאתה מחפש את ה- ♣Q, אבל המידע היחיד שיש לך הוא שלמערב יש חמישה קלפי spades ולמזרח יש שניים. זה אומר שלמערב יש שמונה "מקומות פנויים" (קלפים לא ידועים) ביד שלו ולמזרח יש 11. יש יותר מקום ביד של מזרח לאורך ב-clubs, כך, עקוף את מזרח ל-Q.
לקישור – לחץ כאן
עפ"י Andrew Kambites: ספירת מקומות פנויים היא כלי שימושי, אבל רק כאשר חסר לך בדיוק קלף אחד בסדרה בזמן שאתה מקבל את ההחלטה הקריטית. זה לא תמיד נותן את התמונה המלאה.
לקישור – לחץ כאן (עמ' 44)
לקישור לשיעור " Using vacant spaces in bridge to improve our finessing " ב-youtube – לחץ כאן
לקישור לשיעור " Vacant Places – Bridge Hand Of The Week " ב-youtube – לחץ כאו
לקישור לשיעור " ?Opening leads, Vacant Places, and covering an honour with an honour " ב-youtube – לחץ כאן
לקישור לשיעור " Vacant spaces edition " ב-youtube – לחץ כאן
עפ"י ניתוח יד של Tim Bourke בכתבתו בכותרת " Vacant Places " של Fernando Lema מארגנטינה שנבחר כחבר במועצת המנהלים של WBF-World Bridge Federation בנובמבר 2020.
Tim Bourke הוא שחקן ברידג' אוסטרלי שזכה בתשעה תארים לאומיים אוסטרליים, וסופר ברידג' אוסטרלי. הפרויקט המשותף שלו עם Justin Corfield בשם "האמנות של משחק הכרוז-The Art of Declarer Play" זכה בפרס ספר השנה הבינלאומי לעיתונות ברידג'-The International Bridge Press Book ב-2014. אוסף ספרי הברידג' של Tim ו-Margaret Bourke נחשב לגדול מסוגו (בשפה האנגלית) בעולם. בני הזוג, שניהם שחקני ברידג' מפורסמים תרמו את האוסף ל-State Library of Victoria, החל משנת 2008.
המכרז:
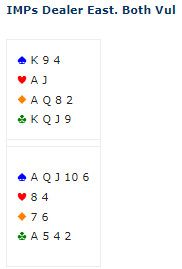
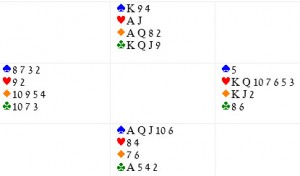
לאחר ה-overcall המעט עליז-נמרץ של דרום, צפון הגיע לסלאם קטן דרך Roman Key-Card Blackwood. דרום הודיע על 2 קלפי מפתח וה-Q בסדרת השליט בהכרזת ה-5spades שלו, ולאחר מכן שלל שהוא מחזיק ב-K בסדרה צדדית ע"י הכרזת 6spades.
מערב הוביל את ה-9, מה שהיה עקבי עם החזקת doubleton. הכרוז לקח את זה עם ה-A של הדומם ואז הוציא את ה-K ואת ה-A בסדרת השליט, ובכך גילה את החלוקה של 4-1 בסדרה. הכרוז הניח שבידו של מערב 6-קלפים ב-Major's ל-8 של מזרח. לפי העיקרון של מקומות פנויים, הכרוז ידע שלמערב יש שבעה מקומות כאלה ל-K diamonds לעומת החמישה במזרח: לעקיפת ה-diamonds הייתה אם כן סיכוי של כמעט 60% לזכות.
החלוקה המלאה:
מקור: youth.worldbridge – לקישור – לחץ כאן
עפ"י ניתוח יד של Justin Corfield: כאשר שאר הדברים שווים, יש סיכוי של 36% שסדרה תתחלק 3-3, סיכוי של 28% לחלוקת 4-1 (למרות שזה מרגיש כמו יותר), סיכוי של 50% שעקיפה פשוטה תצליח (אם כי לפעמים זה מרגיש כמו פחות) וכן הלאה. החוכמה היא לדעת אילו 'דברים אחרים' עשויים שלא להיות 'שווים'. האמת, לעתים רחוקות הם כאלה.
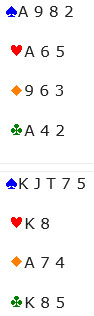
אתה בחוזה של ♠4, לאחר מכרז ללא עוררין-ללא התערבות היריבים בהובלת club ממערב. אתה מוזמן להפסיד 2 קלפי diamond ו-club, ולכן כדי להצליח, תצטרך לשחק את סדרת ה-spade ללא הפסד. לזרוק את ה-A-K הוא ללא ספק הטוב ביותר. אתה תצליח בכל פעם שה-spades יהיו 2-2 ובכל זמן שה-Q היא singleton. (אתה תצליח גם אם ה-spades הם 4-0, כל עוד אתה מנחש מאיזו יד להתחיל). כמובן, הנסיבות משנות את המקרים. נניח שאתה מחזיק באותם קלפים אבל מזרח פתח עם הכרזת מנע-pre-emptive של ♥4. האם זה משנה את האופן שבו אתה צריך לשחק את סדרת ה-spade?
אתה בטוח שכן! כעת המשחק הטוב ביותר הוא לפדות את K ה-spade, מתוך כוונה לעקוף את מערב עבור ה-Q. הסיבה לכך היא זו: ברגע שאתה יודע שלמזרח יש סדרת hearts ארוכה מאוד, הוא מדורג להיות קצר יותר ממערב בשאר הסדרת. חשוב על זה ככה – למזרח כנראה יש 8 קלפי hearts, ולכן 5 קלפי 'לא hearts'. למערב כנראה אין קלפי hearts, ולכן יש לו 13 קלפי 'לא hearts'. ה-Q spades, בהיותה spade, היא 'לא heart. זה גורם למערב (שיש לו 13 קלפים כאלה) לבעל סיכוי גבוה יותר לקבל אותו מאשר למזרח (שיש לו רק חמישה). עבור המחצית הראשונה של העיקרון – אורך מושך מחסור – זה הכי רחוק שאנחנו צריכים ללכת. למחצית השנייה – עיקרון המקומות הפנויים – אנחנו צריכים להסתכל יותר מקרוב, לספור את הקלפים שכל מגן שיחק.
נניח שאתה לוקח את ה-K club, גובה את ה-K spade (כולם עוקבים), וממשיך עם ה-J, עליו משחק מערב את קלף ה-spade הנמוך שנותר. מה הסיכויים אם אתה עוקף? ובכן… ראינו שניים מחמשת הלא-hearts של מזרח (club ו-spade) משאירים אותו עם שלושה 'מקומות פנויים', או קלפים לא ידועים. ראינו שלושה מתוך שלושה עשר ה-hearts של מערב (club ו-2 spades), ומשאירים אותו עם עשרה. אז, ברגע המפתח, העקיפה היא פייבוריטית של עשר עד שלוש – סיכוי של 77%. זה, בקצרה, העיקרון של מקומות פנויים. (יש כאלה שיתעלמו מה-clubs בחישוב מכיוון שמערב היה צריך להוביל משהו ומזרח היה צריך ללכת בעקבותיו, אבל זו נקודה קטנה).
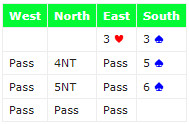
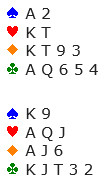
במוקדם או במאוחר, תצטרכו להתמודד עם יד כמו זו ביד הבאה. השותף מכניס אותך ל-♣7, וזה מה שאתה רואה:
הכפילות ב-Major's היא חוסר מזל של מה בכך. אילו ידעת, היית עוצר ב-6NT. בינתיים, מערב מוביל ב-heart וזה תלוי בך למצוא את ה-Q diamonds. בשלב זה, יש לך ניחוש פשוט של 50-50 היכן היא נמצאת. האם נוכל לשפר את זה? אולי אנחנו יכולים. נניח שאתה מושך שליטים, מזרח מגיע עם שלושתם. הסיכויים לעקיפת ה-diamonds השתנו כעת. למזרח יש עשרה 'לא-clubs' לשלושה עשר של מערב, מה שהופך אותו למועדף בין שלוש עשרה לעשרה, או 57%, לשחק על מערב עבור Q diamond. רוב העקיפות מתחילות את החיים בסיכויים של-50-50 , אבל מעט מאוד מהן נשארות כך. כדי להעביר את הזמן, אתה מחליט לפדות את יתרת הזוכים ב-spade וב-heart. מזרח מפתיע אותך בשלב זה ע"י השלכת spade בסיבוב ה-hearts השלישי. כעת אנו יודעים שמזרח התחיל עם שלושה clubs, שני hearts ושניים או יותר spades, והותיר אותו עם שישה מקומות פנויים, בעוד שמערב התחיל ללא clubs, שישה hearts ושני spades או יותר, והותיר אותו עם חמישה מקומות פנויים. הסיכויים בסדרת ה-diamonds השתנו שוב ומזרח הוא כעת בעדיפות של שישה עד חמישה, או 55%, להחזיק ב-Q diamond. מעבר ל-K diamonds והרצת ה-T הוא המשחק הטוב ביותר.
מסקנה: הסיכויים שדבר נתון יקרה אינם חקוקים באבן – להיפך, במהלך משחק רוב הידיים, על הכרוז להתעמת עם תמונה משתנה. האחוזים שנתן הכותב בתחילת כתבתו זו נכונים לחלוטין. הם הסיכויים שדבר נתון יקרה בהנחה שאיננו יודעים דבר על הידיים הנסתרות. ברגע שהמידע מתחיל להגיע, הסיכויים האלה יכולים להשתנות ולעתים קרובות משתנים.
לקישור לכתבתו בכותרת " Length Attracts Shortage: The Principle of Vacant Spaces " – לחץ כאן
לקישור לכתבה " The theory of vacant places " – לחץ כאן
לקישור ל " Vacant spaces and significant cards in odds calculation " בכתבה " On the Use of an Odds Calculator " – לחץ כאן
לקישור לניתוח יד בכותרת " A Vacant Spaces Calculation " לחץ כאן
לקישור לניתוח יד בכותרת " Vacant places vs missing points " בפורום BBO – לחץ כאן
לקישור לניתוחי ידיים בכותרת " Vacant spaces " – לחץ כאן וכאן
לקישור לניתוח יד בכותרת " ?Vacant Spaces or Restricted Choice " -לחץ כאן
לקישור לניתוח יד בכותרת " Modified Vacant Spaces " – לחץ כאן
לקישור לניתוח יד בכותרת " Applying Vacant Spaces to Distributional Hands " – לחץ כאן
לקישור לניתוח יד בכותרת " Vacant Spaces Principle " – לחץ כאן
לקישור לניתוח יד בכותרת " 'My Subjective 'Solution' to 'The Greatest Play " -לחץ כאן
לקישור לניתוח יד בכותרת " Space: Beyond the Frontier " – לחץ כאן
לקישור לניתוח יד בכותרת " Vacant Thinking " – לחץ כאן
לקישור לניתוח יד של מועדון Oxford Club בכותרת " מפגשים מהסוג השלישי " (עמ' 5) – לחץ כאן
לקישור לניתוח יד בכותרת " Logical Thinking In Bridge " (עמ' 8) – לחץ כאן
לקישור לניתוח יד –ב-Alert April 3, 2023 (עמ' 11) – לחץ כאן
לקישור לניתוח יד-משאל בכותרת " …If only it was as simple as vacant spaces " – לחץ כאן
לקישור לטבלת " הסיכויים לחלוקת קלפים מוסתרים-חבויים בידי היריבים " באתר " 60secondbridge " – לחץ כאן
לקישור לכתבה " The Vacant Spaces Trap " לחץ כאן
לקישור לכתבה " ?The Theory of Vacant Spaces " – לחץ כאן
לקישור לכתבה " Monty Hall, Restricted Choice & Vacant Spaces " – לחץ כאן
לקישור לכתבה " The nature of bridge probabilities 2 " – לחץ כאן
לקישור לכתבה " Fire and Ice: Properly Evaluating Information at the Bridge Table " – לחץ כאן
לקישור לכתבה " Restricted Choice vs Vacant Spaces " – לחץ כאן
לקישור לכתבה " Vacant Spaces " – לחץ כאן
לקישור ל " Suit Break Calculator " – לחץ כאן
ולהשלמת התמונה :
עפ"י דרור שיפטן: עקרון הבחירה המוגבלת-Choice Restricted הוא עיקרון סטטיסטי שלפיו כאשר שחקן משחק קלף, ההסתברות שהוא מחזיק קלף שווה ערך קטנה יחסית. עיקרון זה מבוסס על חוק Bayes, שלפיו הסתברות של התרחשות אירועים מתעדכנת על פי מידע שמצטבר. דרך פשוטה יותר להסביר את העיקרון היא, ששחקן המחזיק J בודד חייב לשחק אותו, אבל שחקן המחזיק QJ doubleton צפוי לשחק Q ב-50% מהזמן ו-J ב-50% מהזמן. במלים אחרות, אם כבר ידוע שה-J שוחק, רוב הסיכויים הם שזה היה קלף בודד שלא הייתה ברירה אלא לשחקו.
לקישור לכתבתו " לעקוף או לא לעקוף (חלק ג') " בגיליון אפריל 2014 של התאגדות ישראלית לברידג' (עמ' 16) – לחץ כאן; לקישור לחלק החמישי והאחרון של כתבתו בגיליון ספטמבר 2014 של התאגדות ישראלית לברידג' (עמ' 22) – לחץ כאן
לקישור לכתבה " עקרון הבחירה המוגבלת-The Restricted Choice " – לחץ כאן
בברכה,
גבי לוי
